上学期的一天，我在开发区初中听了曹文娟老师的数学课。曹老师选岗分配到初中后第一年教初一，第二年教初二。现在是第三年了，她任教初三数学。

　　初一、初二时，我听过几堂课，感觉上得不错。初三上学期她被推荐参加临城学区的优秀课比赛，获得参加高邮市比赛资格。在高邮市青年教师优秀课评比中，她又摘得了一等奖。因此非常想再听听她的课。

　　她上的是复习课，复习内容是全等三角形。她让学生预习课本内容3~4分钟，然后提出一些问题让学生回答，属正常问答。在例题训练时，发现她有长处，一是让学生当堂说出思路，二是让学生说出不同的解题方法，三是让学生思考有无更简便的解题方法，四是让学生当堂完成作业训练，五是学生课后无更多的作业负担。我认为现在提倡的有效课堂教学，她体现了；课堂当堂作业、当堂训练、当堂完成了，她体现了；减轻学生过重课业负担，她体现了；贯彻扬州市教学质量效益年精神和高邮市高效课堂推进的要求，她体现了。

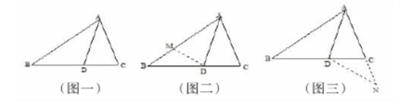
　　有一条复习题留给我的影响非常深刻。“在△ABC中，已知AB＞AC，AD平分∠BAC，求证：AB－AC＞BD－DC（如图一）”。学生经过一番讨论后，有在AB边上截取AM＝AC，求证△ADM≌△ADC后，得出CD＝MD，再利用“三角形任意两边之差小于第三边”的原理而得出结论（如图二）。也有延长AC边使AN＝AB，连接DN，求证△ABD≌△AND，得出BD＝ND，再利用三角形上述的原理得出结论（如图三）。

　　在老师问还有没有解法时，一个男生提出了另一种解法：

　　在△ABD中，AB＋AD＞BD，①

　　在△ACD中，AC＋AD＞DC，②

　　因为AB＞AC，所以用不等式①减去不等式②，不等式左边减去左边，右边减去右边，即可得AB－AC＞BD－DC。

　　听到这种解法，我为这个男生的聪明叫好，尽管这种解法有漏洞，尽管这题解法有已知条件没有用，但我还是从内心对这名男生产生敬意。

　　曹老师虽然是年轻教师，但遇到这种情况倒显得很沉稳，很老练。她没有被这题所迷惑，她没有因为遇到这“难题”而慌乱，她在鼓励这名男生能想到这么简单的解法后，很睿智地解决了这种解法的不严密性和不科学性。她说：不等式没有这种性质。她用数字进行例证证明了这种解法的不成立。例如：7＞5，6＞2，这两个不等式，且7＞6，用7＞5不等式和6＞2不等式的左边减左边，右边减右边，所产生的一个新的不等式能否就成立呢？1＞3显然不成立。

　　这位男生的这种解法看上去很简捷，结果很巧合，尽管解法有漏洞，可我为这名男生的解法叫好，为这名男生的聪明叫好。曹老师能当堂应急，在鼓励学生、肯定学生的同时，也很睿智地解决了这个问题。课后与曹老师交流时，她说当时内心还是比较紧张的，但在课堂上她表现出的是机智、是沉稳、是对学生的赞扬。我也为曹老师的沉稳叫好，为曹老师的睿智叫好！